『球と円柱について』(ギリシア語 Περὶ σφαίρας καὶ κυλίνδρου )は、紀元前225年ごろアルキメデスにより発表された2巻からなる著作 。 最も注目すべきは、球面の表面積や球体の体積、円柱のそれにあたる値を見つけ出す方法が詳しく書かれていることであり、アルキメデスはこれ半球の体積は、球の体積 の 例題1:半径が $3\\mathrm{cm}$ の半球の体積を計算してみましょう。 公式を使うと、 $\dfrac{2}{3}\times\pi\times 3\times 3\times 3=18\pi\\mathrm{cm}^3$ と計算できます。 円周率 $\pi$ はおおよそ $314$ なので、半球の体積はおおよそ、 $18\times 314=5652\\mathrm{cm}^3$ となります。 半球 球の体積 体積V = 4 3πr 3 目標:上式で求まる理由を知る( 積分 等の高校数学を使わずに) はじめに 球の体積 方法①:微小な四角錐を考える 考え方 方法②:カヴァリエリの原理を使う カヴァリエリの原理
球缺体积公式 推导球缺的体积公式 尚书坊
球 体積 公式
球 体積 公式-体積 = 半径 × 半径 × 314 × 高さ 面積= πr × 2πr × 1 2 = π2r2 = 314πr2



球缺体积公式 推导球缺的体积公式 尚书坊
円がぴったり 入る円柱 円がぴったり 入る円柱 球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める 具体物での実験をもとに公式を導きます。 こんにちは。相城です。今回は球の体積の何で?にお答えできればと存じます。 球の体積の公式のなぜ? 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しくなる。 つまり、球の体積を微分すると円の表面積の公式になります。 そもそも微分とは、『少しの増加の間の変化量』を表現しています。 円の面積のちょこっとの増加分は円の周りの長さに相当します。 球の体積のちょこっとの増加量は球の表面積に相当します。
313 体積の計算 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換 3 13 体積の計算 例 3 63 (球の体積) 半径 の球の体積は である. これを多重積分で求める. (その 1) 球を 8 等分し底面が であり,上面が の体積 として求める. 2 次元の極座標 , とおくと, 領域Sをcを使わずに、S=(2*pi*r)*(h)とした方が解りやすいのではないでしょうか。これは、球の表面積は、「それがずっぼり入る円柱」側面の表面積に等しい、というアナロジーから導かれるのでは。 0728 男/50歳代/研究員/役に立った/ 使用目的 部分球の体積計算公式集 (面積・体積・・) 公式集-断面性能 記号-単位 ちょっとよりみち 物理学ハンドブック 公式集-乗法公式・因数分解 楕円体 楕円面 で囲まれた空間の部分を楕円体という。 楕円体 主軸の長さが 2a、2b、2c のとき 楕円体の体積 体積 V = 4π a b c /3 楕円体の表面積 (楕円面の表
次へ 球の体積 関連トピック 定積分;球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume8、円錐台の体積の公式 目次にもどる 人類はどうやって球の体積を求めたのか 1、アルキメデスは球の体積をどうやって見つけたの? T:球の体積は半径をrとすると、4/3・π・r 3 で求めることができるんです。覚え方は、『3分で忘れる心配あーるの参上。』『身の上に心配あーるのさん



球缺体积公式推导图解 万图壁纸网




球体积公式
球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) \(\displaystyle \frac {6}{D \rho}\) 半分以上隠れている円の直径の推定 接触角の概算 円と球の空間 これで球の体積の公式が理解できましたね。 極限まで小さくすると歪んだ面積が四角形にみなすことができ、それをもとにして微小な体積を足し合わせると歪んだものでも、体積を求めることができるという考えが 積分 です。 高校数学の最終章 です。V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin




球体积公式计算器 计算器在线 转换器




球的体积公式推导图文 如何用微积分知识推导球的体积公式 三人行教育网 Www 3rxing Org
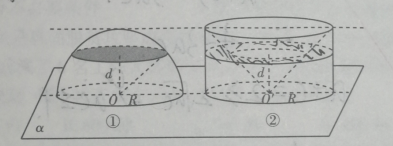
よって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積球の体積を計算してみます。ある点(中心)から、表面のどの点までの距離も等しい物体を球と呼びます。 球の体積は、中心から表面までの距離(常に一定)を半径rとすると、 4/3 * π * r 3 であらわされます。πは、円周率のことです。円周率は と続きます。実際の計算では、314 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め



圆球表面积 球体表面积的公式证明 篆体字转换器
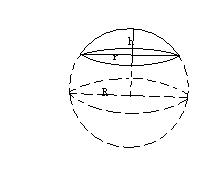



球缺 维基百科 自由的百科全书
球の体積と表面積の公式 半径 r r r の球の表面積は S = 4 π r 2 , S=4\pi r^2,\ S = 4 π r 2 , 球の体積は V = 4 3 π r 3 V=\dfrac{4}{3}\pi r^3 V = 3 4 π r 3 である。 球の体積や表面積、忘れがちですよね。 昔、私が学生の時に学校の先生にこんな覚え方を教わりました。 なかなか覚えられないかたはぜひ!(笑) ※覚え方 表面 に 心 配 あるある 表面積 4 π r² ⑧球の体積の公式 : 4/3πr³ 球の体積の公式には以下の有名な語呂合わせがあります。 「 身 (\(3\)) の上に心 (\(4\)) 配 (\(\pi\)) アール (\(r\)) の \(3\) 乗 」 公式を覚えるのが苦手な人は、語呂で覚えてもよいかもしれませ



球体积怎么求公式 百度经验



圆球体积公式 球的体积和表面积 趣闻趣事网
球の体積の公式をつかいましょう!球の体積の公式は、4πr 3 / 3でしたね。 4πr 3 / 3 にr=3を代入します。 4π×3 3 / 3 = 36π・・・(答) となります。簡単ですよね? 球の体積の公式は必ず覚えましょう! 球の表面積に関する問題 柱の体積 = 底面積 × 高さ 表面積 = 底面積 × 2 側面積 3球の体積 4楕円体の体積 解法 a直接積分する b微小面積(体積)を幾何学的に計算して積分する方法 cヤコビ行列を使用する方法 チェックを入れた方法(aとbとcの方法)で計算して、公式と一致しているかどうかを確認しようと思います。



球体体积公式 怎样计算球体的体积



圆球表面积 球体表面积的公式证明 篆体字转换器
公式を導く算数教科書の記述の背景にある,高校数学 の内容について論じている(pp5460)。 また,円の面積公式や球の体積公式の導出に関して, 現在までに幾つかの実践研究が行われている。例えば, 廣瀬ほか(13)は,極限の考えを取り入れた円の面 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう! ←今回の記事 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! 頑張っているのに思うように成績が上がらず、 「このままだと本番で数学60点が厳しいかも」 と不安に感じているあなた。 もしか



球的体积公式推导 学步园



悟空问答 为什么球体积公式对半径求导是球面积公式 而圆面积公式对半径求导又是圆周长公式 9个回答
球の表面積を積分 = 球の体積 逆に、 円の面積を微分 = 円周 球の体積を微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するため 球の体積の求め方 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を代入して




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网
球の体積を求める公式は、V = 4/3 πr^3 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。
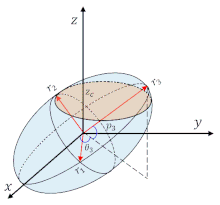



椭球 维基百科 自由的百科全书



球的体积公式推导证明 资优网




球面積積分球的體積 Itha




求球体的表面积和体积 修也 Csdn博客




如何计算球的体积 5 步骤



球的体积公式球的体积公式是什么



球體體積 總表面面積 Youtube



球缺体积公式 推导球缺的体积公式 尚书坊




球缺体积球缺的体积公式



球的面积和体积公式 西瓜视频搜索




表面积公式球



物理方法解决数学问题 二 Archimedes与球体积公式 Matrix67 The Aha Moments
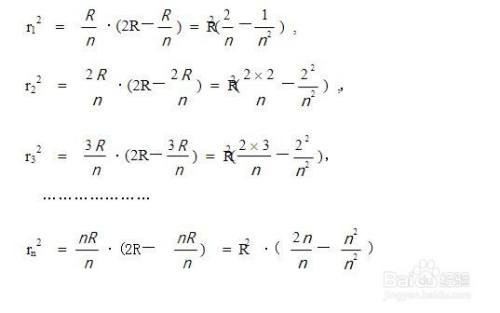



球体体积公式推导图解 百度经验




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




如何计算球的体积 5 步骤



在球的体积公式中 为什么会出现三分之四这个奇怪的



高中数学牛x 公式 利用三棱锥内切球的半径与体积关系式快速解题 努力学习网




用感覺理解球體表面積公式 Youtube




球表面積公式球體表面積 百度百科 Kmbymh



球的表面积公式 球的表面积公式画法



在球的体积公式中 为什么会出现三分之四这个奇怪的




球相交的表面积并 体积并 Jzk Keven 的博客 Csdn博客




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com




原 C 公式 计算球弧面体积 球缺 南水之源 博客园




中国古代数学思想 读书笔记 23 文章




球体表面积及体积的推导 每日头条




球体积公式表面积推导过程是什么多少计算公式 小街网



球的體積




头条文章



为什么对球的体积公式求导就是球的面积公式




三重积分求球体积 三重积分用极坐标怎么计算球体体积 三人行教育网 Www 3rxing Org




塑料空心球重量与塑胶空心球体积的计算公式 News



1



漫谈超球体的体积公式 知乎



多维球体的体积 小时百科




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



简单的数学 初中生也能推导球的体积公式 叫我笑笑 哔哩哔哩 Bilibili



球的体积转立方米公式 圆球体积计算公式 公式学习




積分球公式球的體積 Jvvx




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com



圆球体积公式 球的体积和表面积 趣闻趣事网



定积分椭球体积公式 定积分推椭球体积公式 用定积分推出椭球体积
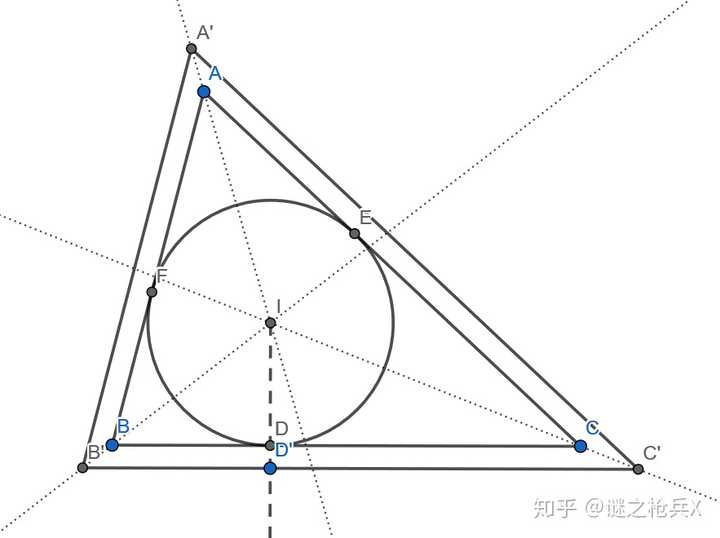



求球体积公式 圆球的体积公式 求球体积积分公式



1



椭球体积公式推导 作业帮




012 球的体积空间几何体高中数学 Youtube



表面积体积公式大全 搜狗图片搜索




體表面積表初中數學 幾何 面積與體積公式 Uhlwc




球的表面积和体积怎么算啊怎么计算球的表面积



圆球体积公式 球的体积和表面积 趣闻趣事网



球的体积公式 万图壁纸网
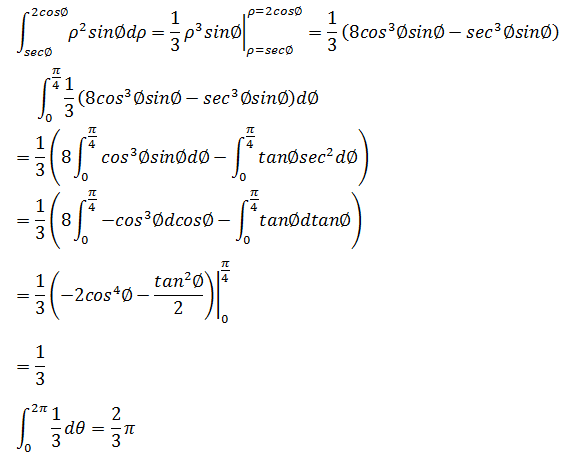



多变量微积分笔记 球坐标系 我是8位的 博客园




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球の体積と表面積 Youtube



基于高速摄影测量气泡体积的图像处理技术研究



Q Tbn And9gcqzkudsal3galmxwro65pdnhz6flxjjkxas5i6eaqlha2sgymk7 Usqp Cau
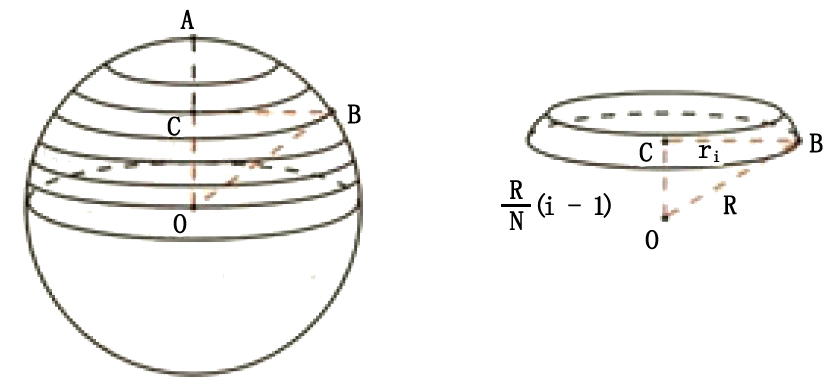



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客 球的体积公式



圆球体积公式 球的体积和表面积 趣闻趣事网




圆面积与球体积的统一探讨 参考网



圆球体积计算公式球体积公式球的体积计算公式为43pr3 求半径为3 5cm的球的体积 P取3 14 结果保留五个有效数字 爱华网



一个单位球体积搞定二三重积分 哔哩哔哩 つロ干杯 Bilibili
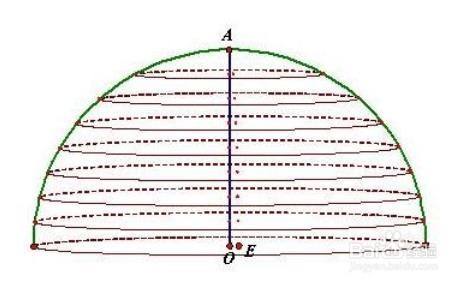



球体体积公式推导图解 百度经验




球体体积公式推导图解 搜狗图片搜索




微積分150 橢球的體積 Youtube



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




高中数学必修二经典考题 球的表面积和体积 含答案 三好网




橢球 一種二次曲面 是橢圓在三維空間的推廣 橢球在xyz 笛卡兒坐標系中的方程是 X 華人百科



球体积的前世今生 新华网



球体积公式照片 正版商用图片1dbb8d 摄图新视界



1




N维球体 N维椭球体体积公式证明 Kol Mogorov的博客 程序员宅基地 N维椭球体积公式 程序员宅基地
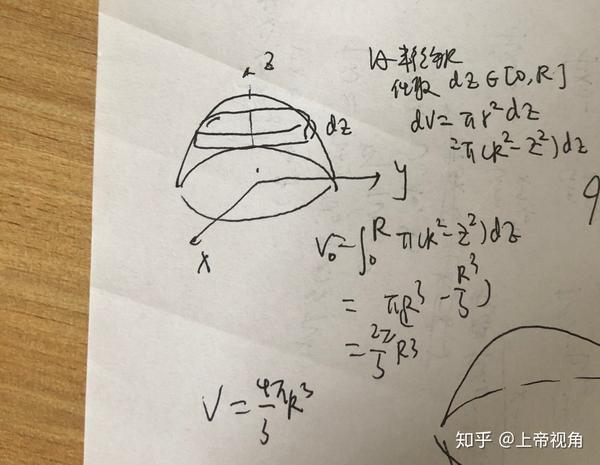



在推导球的体积公式时 将球的体积视为截面圆的积累进行积分运算 可行吗 椭圆球体体积公式积分推导 双偶网



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




球体的表面积和体积的计算公式 星火网校



球缺体积公式 推导球缺的体积公式 尚书坊




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org



球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org



球体积推导例题 球的体积公式推导过程 密度体积网



球体体积公式是球体体积公式是什么



球的体积公式和表面积公式 高三网



球体体积公式教学 西瓜视频搜索




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org




外接球体积的常见套路 几何 知乎



数学一分钟球的体积公式推导证明 哔哩哔哩 つロ干杯 Bilibili




證明球體體積公式 Youtube




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科
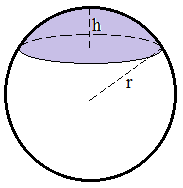



球冠体积 表面积在线计算器



塑料圓球重量計算與塑膠圓球體積公式 尚书坊



N 维超球体积公式 哔哩哔哩 Bilibili



0 件のコメント:
コメントを投稿